Demostración Formal: Suma y Silogismo Aristotélico

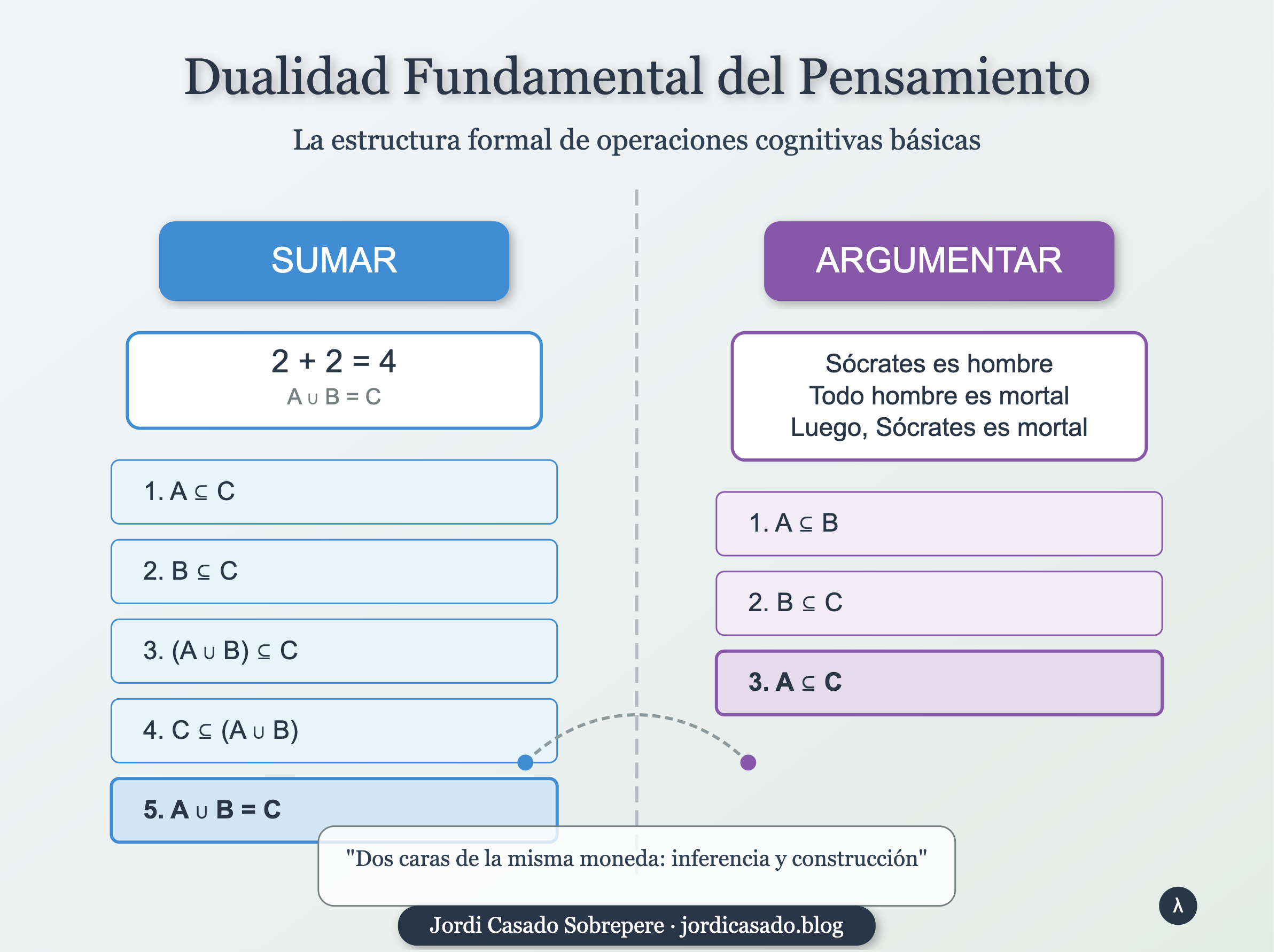
Operaciones Cognitivas Fundamentales

1. SUMAR (Demostrar que A + B = C)

Ejemplo concreto: 2 + 2 = 4

Queremos demostrar formalmente que:

• A (el conjunto/propiedad «2») unido con
• B (otro conjunto/propiedad «2») es igual a
• C (el conjunto/propiedad «4»)

Paso	Demostración	Justificación
1	A ⊆ C	Premisa inicial
2	B ⊆ C	Premisa inicial
3	(A ∪ B) ⊆ C	Ver apéndice (*)
4	C ⊆ (A ∪ B)	Ver apéndice (**)
5	A ∪ B = C	Por doble inclusión (3, 4)

2. ARGUMENTAR (Silogismo Aristotélico)

Ejemplo concreto: Sócrates es un hombre, todos los hombres son mortales, luego Sócrates es mortal.

Formalmente:

• A (Sócrates) está incluido en B (conjunto de hombres)
• B (conjunto de hombres) está incluido en C (conjunto de mortales)
• Por lo tanto, A (Sócrates) está incluido en C (conjunto de mortales)

Paso	Demostración	Justificación
1	A ⊆ B	Premisa inicial
2	B ⊆ C	Premisa inicial
3	A ⊆ C	Por transitividad

---

Apéndice Explicativo

(*) Explicación paso 3 (Suma): La inclusión (A ∪ B) ⊆ C se establece porque todo elemento que pertenece a la unión A ∪ B debe pertenecer a A o a B (por definición de unión). Dado que A ⊆ C y B ⊆ C (premisas 1 y 2), cualquier elemento de A está en C y cualquier elemento de B está en C. Por tanto, cualquier elemento de A ∪ B debe estar necesariamente en C, lo que establece que (A ∪ B) ⊆ C.

En el ejemplo numérico 2+2=4, esto significa que todos los componentes que forman el «2» y otro «2» están necesariamente contenidos en el «4».

() Explicación paso 4 (Suma)**: La inclusión C ⊆ (A ∪ B) se establece porque se asume que C está completamente compuesto por elementos de A y elementos de B, sin elementos adicionales. En términos aritméticos, esto equivale a asumir que 4 no es mayor que la suma de 2 y 2. Esta es una propiedad fundamental de la suma: el resultado no contiene más que lo que aportan sus sumandos. Por tanto, cada elemento de C debe pertenecer a A o a B, lo que establece que C ⊆ (A ∪ B).

---

Comparación Estructural

La comparación entre ambas demostraciones revela la estructura fundamental de dos operaciones cognitivas básicas:

1. Suma: Establece una igualdad (A ∪ B = C) mediante verificación de doble inclusión

   • En el ejemplo: 2 + 2 = 4 se demuestra verificando que 2∪2 ⊆ 4 y 4 ⊆ 2∪2

2. Silogismo: Establece una inclusión simple (A ⊆ C) mediante transitividad

   • En el ejemplo: «Sócrates es mortal» se demuestra mediante la transitividad de las inclusiones «Sócrates ⊆ hombres» y «hombres ⊆ mortales»

Esta simulación constructivista revela cómo las operaciones mentales fundamentales pueden modelarse mediante manipulaciones formales de conjuntos, mostrando la profunda unidad entre el pensamiento matemático y el razonamiento lógico aristotélico. Además, evidencia que la suma aritmética ya incorpora inherentemente pasos de inferencia deductiva en su estructura formal.